続・わかりやすいパターン認識ひとり読書会 3 - 渡邊哲司（Satoshi Watanabe）の日記

今回は実際に実装したディリクレ過程混合モデルの挙動を見ていきます。

続パタ読書会 1:ディリクレ過程混合モデル
 続パタ読書会 2:ディリクレ過程混合モデルのアルゴリズム
続パタ読書会 3:実験
続パタ読書会 4:実装
 続パタ読書会 5:事前確率P(s)の妥当性 1
続パタ読書会 6:事前確率P(s)の妥当性 2
続パタ読書会 7:ベル数 1
続パタ読書会 8:ベル数 2
続パタ読書会 9:P(s_k|x_k, s_-k, θ)の導出
 続パタ読書会 10:演習問題12.5の計算
 続パタ読書会 11:演習問題12.6の計算 1
続パタ読書会 12:演習問題12.6の計算 2

実験

前提

実験は下記の前提で行いました。

総学習回数 $100$ 回
打ち切り回数 $30$ 回

つまり30回更新が滞れば総学習回数の100回に満たずとも収束したと判断して学習を終了します。ハイパーパラメータはテキストに倣い

$\alpha=1.0$
$\beta=\displaystyle\frac{1}{3}$
$\nu=15$
$\mathbf{S}=\begin{bmatrix}0.1&0.0\\0.0&0.1\end{bmatrix}$

としてます。またパターンは下記より確率的に生成した混合正規分布のパターンを用いました。

総パターン数 $n=500$
クラスタ数 $c=5$
特徴空間の次元数 $d=2$
各クラスタの所属確率

$\boldsymbol{\pi}=\begin{bmatrix}0.4, 0.2, 0.2, 0.1, 0.1\end{bmatrix}$ （ $n_i=\begin{bmatrix}200, 100, 100, 50, 50\end{bmatrix}$ と同義）

各クラスタの平均

$\mu=\begin{bmatrix}\left(\begin{array}{c}-3.0\\3.0\end{array}\right), \left(\begin{array}{c}2.0\\4.0\end{array}\right), \left(\begin{array}{c}0.0\\0.0\end{array}\right), \left(\begin{array}{c}4.0\\-2.0\end{array}\right), \left(\begin{array}{c}-2.0\\-4.0\end{array}\right)\end{bmatrix}$

各クラスタの分散共分散行列

$\mathbf{\Sigma}=\begin{bmatrix}\begin{bmatrix}0.4&-0.4\\-0.4&0.6\end{bmatrix}, \begin{bmatrix}0.7&0.6\\0.6&0.6\end{bmatrix}, \begin{bmatrix}0.3&0.2\\0.2&0.5\end{bmatrix}, \begin{bmatrix}0.3&0\\0&0.3\end{bmatrix}, \begin{bmatrix}0.5&0.1\\0.1&0.5\end{bmatrix}\end{bmatrix}$

実際に実験時に生成されたパターンは以下のようなものです。

f:id:SatoshiWatanabe:20190518150934p:plain:w500

ここで楕円は $\sigma=3$ の範囲を表しています。

結果

結果として44回目の学習時に対数事後確率は最大の $-1701.3$ になり、その時点のクラスタ数は正しい5つでした。以後更新は停滞したまま74回の学習で終了しました。
学習の経緯を下記に示します。下側にある二つのグラフは対数事後確率の値とクラスタ数で、対数事後確率が最大になった44回の時点には赤い破線が入るようにしています。

f:id:SatoshiWatanabe:20190518151335g:plain:w500

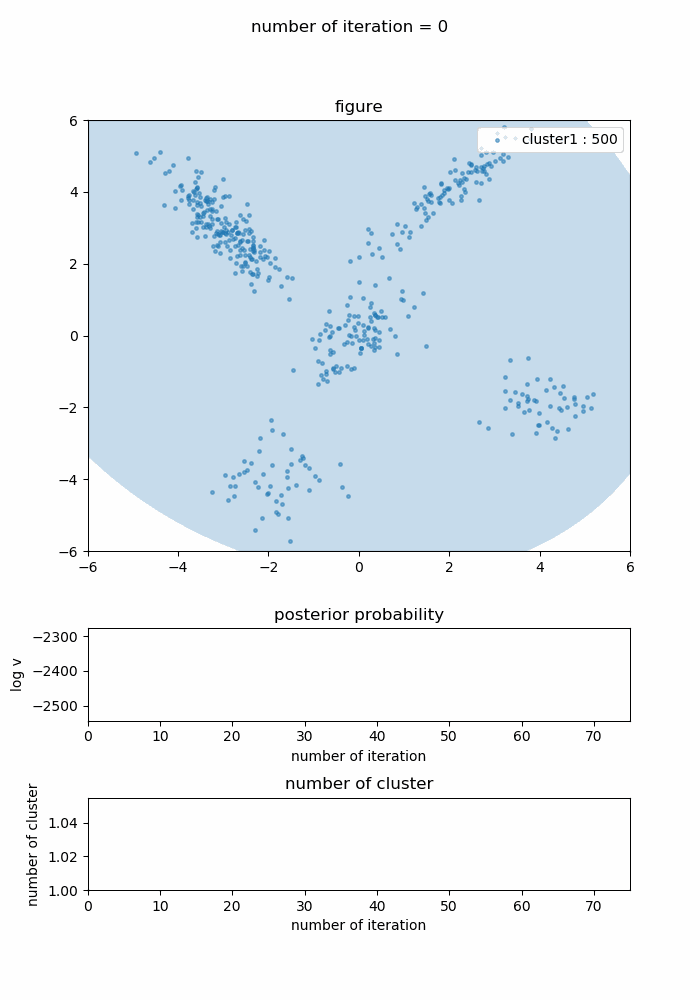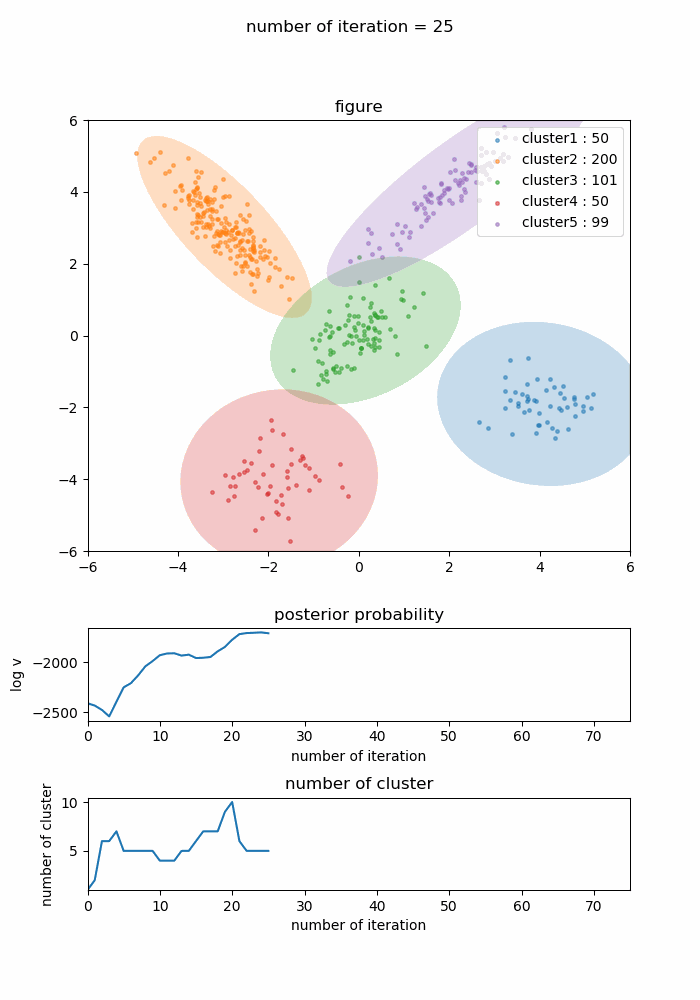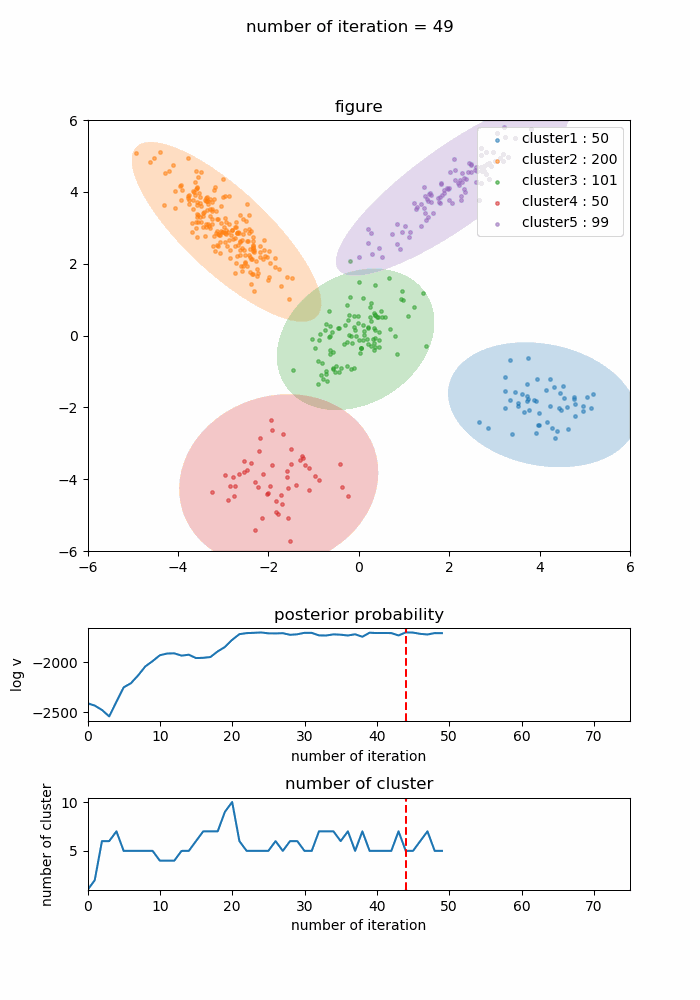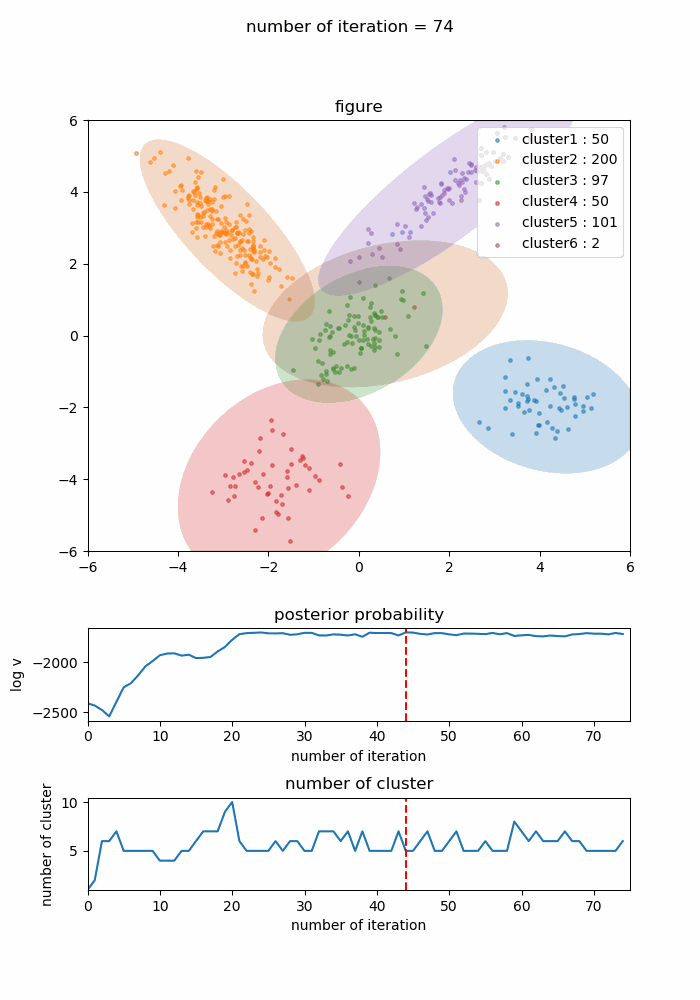
この学習経緯を見ると徐々に正しいクラスタリング結果に近づき、対数事後確率が最大になって以降はその状態からクラスタ数やクラスタ形状がピクピク微妙に変化しながらも最適なクラスタリング構造に近い形を維持し続けているのが分かります。対数事後確率が最大になった44回目の状態のみを切り取ると以下のようになります。

f:id:SatoshiWatanabe:20190518155029g:plain:w500

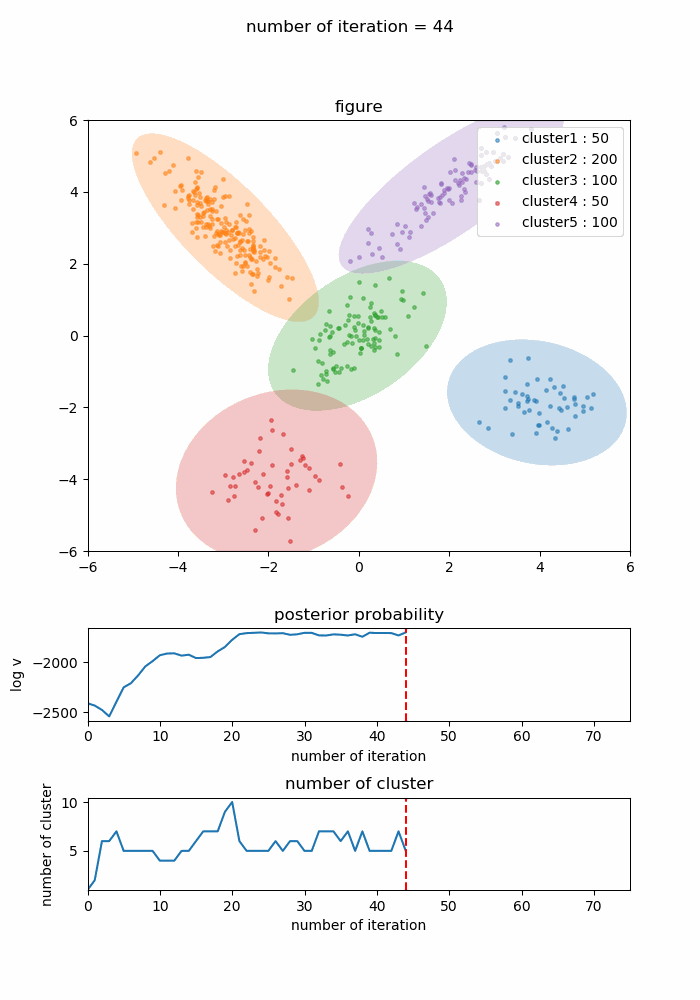
入力と比較して見るとわかる通り正しくクラスタリングされています。クラスタのインデックスの順序は特に意味をなしませんので注意してください。また、クラスタのインデックスを入力と揃えて平均 $\mu$ と分散共分散行列 $\mathbf{\Sigma}$ を比較してみると

入力

予測結果

$\mu=\begin{bmatrix}\left(\begin{array}{c}-3.0\\3.0\end{array}\right), \left(\begin{array}{c}2.0\\4.1\end{array}\right), \left(\begin{array}{c}0.0\\0.0\end{array}\right), \left(\begin{array}{c}4.0\\-1.9\end{array}\right), \left(\begin{array}{c}-1.8\\-3.9\end{array}\right)\end{bmatrix}$

$\mathbf{\Sigma}=\begin{bmatrix}\begin{bmatrix}0.5&-0.5\\-0.5&0.8\end{bmatrix}, \begin{bmatrix}0.7&0.5\\0.5&0.6\end{bmatrix}, \begin{bmatrix}0.4&0.2\\0.2&0.5\end{bmatrix}, \begin{bmatrix}0.4&-0.1\\-0.1&0.3\end{bmatrix}, \begin{bmatrix}0.6&0.1\\0.1&0.6\end{bmatrix}\end{bmatrix}$

となります。予測結果は小数点第二位四捨五入です。まぁ悪くない結果ではないでしょうか。

今回はこのくらいにして次回は具体的な実装内容を書きます。